Este
artigo demonstra como elaborar um Filtro
Digital IIR utilizando o microcontrolador PIC32MX com a DSP Library da Microchip.
Filtros Digitais do tipo FIR (Resposta ao Impulso Finita) e IIR (Resposta ao Impulso Infinita) são muito utilizados por DSPs (Processadores Digitais de Sinais) para a filtragem de sinais.
Semelhantes aos filtros analógicos, os filtros digitais podem ser classificados em 4 tipos quanto à frequência:
- Passa-baixa (lowpass);
- Passa-alta (highpass);
- Passa-banda (bandpass);
- Rejeita-banda (bandstop).
Funções de Janela são utilizadas em Filtros Digitais FIR podendo ser:
- janela Retangular;
- janela de Hamming;
- janela de Blackman;
- janela de Kaiser.
Filtros Digitais IIR podem utilizar modelagem dos filtros analógicos:
- filtro Butterworth
- filtro Tschebyscheff
- filtro Tschebyscheff inverso
- filtro Elliptic
- filtro BesselDe um modo geral os Filtros Digitais IIR são representados pela Equação 1.
Equação 1 - Equação básica para um Filtro Digital.
A Função de Transferência H (z) para um Filtro Digital é vista na Equação 2.
Equação 2 - Função de Transferência H (z) de um Filtro Digital. Fonte: ORFANIDS.
Considerando a0 =1 e M=N=2 obtemos a Equação 3 para um FIltro Digital IIR de Segunda Ordem.
Equação 3 - Função de Transferência para um Filtro Digital de Segunda Ordem. Fonte: ORFANIDS.
A Equação 4 mostra a equação diferencial para o FIltro Digital IIR de Segunda Ordem ou Biquadrado.
Equação 4 - Equação Diferencial para o Filtro Digital de Segunda Ordem. Fonte: ORFANIDS.
A equação diferencial do IIR FIlter Biquad é representada pelo Fluxograma 1.
Fluxograma 1 - Realização do Filtro IIR Segunda Ordem na Forma Direta. Fonte: ORFANIDS
Cada seção biquadrada do FIltro IIR da DSP Library da Microchip para o PIC32MX opera segundo o Fluxograma 2 (Second Order Direct Form II Structure Transposed).
Fluxograma 2 - Operação do FIltro IIR da DSP Library da Microchip. Fonte: Microchip.
Criando um Filtro Digital IIR
A Figura 1 mostra os 3 passos para você criar seu Filtro Digital.
Figura 1 - Passos para criar um Filtro Digital.
Este artigo mostra um exemplo para a construção de 4 tipos de Filtros Digitais IIR:
a) filtro passa-baixa de 1000 Hz;
b) filtro passa-alta de 2000 Hz;
c) filtro passa-banda de 1500 Hz à 2000 Hz;
d) filtro rejeita-banda de 2000 Hz à 2500 Hz.
Vamos a algumas considerações do nosso projeto.
Objetivo do circuito:
Filtrar um sinal entre 0 e 3840 Hz. Aplicar os 4 tipos de filtros IIR para verificar a resposta de cada um deles.
Especificações:
- o sinal de entrada é uma onda senoidal gerada pelo próprio microcontrolador através da equação trigonométrica cos(a+b) = 2 cos a cos b - cos(a-b).
- de acordo com o Teorema de Nyquist, a frequência de amostragem do sinal de entrada será 7680 Hz.
-
o microcontrolador escolhido é o PIC32MX, um microcontrolador de 32-bit da Microchip, que possui as funções para o Filtro
Digital IIR disponíveis na DSP Library. Possui 80 MHz, 512 kB de memória Flash e 128 KB High Speed SRAM.
-
será utilizado o dsPIC Filter Design Lite, um programa de Digital Filter Design, para definir os
parâmetros do filtro digital IIR a fim de obter o sinal filtrado
especificado. O software fornece os coeficientes necessários para o
cálculo do filtro.
-
os coeficientes são utilizados no código fonte C do PIC32. O
programa consiste basicamente em declarar as variáveis,
inicializar os ponteiros e variáveis, iniciar a estrutura do filtro com mips_iir16_setup ( ) e executar o cálculo do filtro digital com mips_iir16
( ).
- é aplicada a transformada Rápida de Fourier (FFT) ao sinal filtrado para verificar a resposta do filtro.
- é aplicada a transformada Rápida de Fourier (FFT) ao sinal filtrado para verificar a resposta do filtro.
-
para teste do nosso circuito o PIC32 varia a frequência do sinal gerado de 0 à 3840 Hz.
- o sinal senoidal gerado e filtrado assim como a FFT são mostrados em um display gráfico.
- o sinal senoidal gerado e filtrado assim como a FFT são mostrados em um display gráfico.
Digital Filter Design: definindo os parâmetros do Filtro Digital
No primeiro passo temos que definir alguns parâmetros para poder utilizar um software capaz de gerar os coeficientes necessários para o cálculo do filtro digital pelo PIC.
Utilizaremos o Filtro Digital IIR Biquadrado (cascata de segunda ordem). Cada IIR FIlter Biquad possui 2 pólos e 2 zeros.
O FIltro Analógico utilizado foi o Butterworth de 4ª ordem. 2 filtros de segunda ordem (biquadrado) em cascata. No total teremos 4 pólos e 4 zeros.
Veja a seguir o Design elaborado para os 4 tipos de Filtros utilizando o dsPIC Filter Design Lite: lowpass, highpass, bandpass e bandstop.
Lowpass IIR FIlter Design
A Figura 2 traz graficamente a representação de cada parâmetro do filtro:
- frequência de amostragem;
- passband;
- stopband;
- máximo ripple no passband;
- mínima atenuação do stopband.
Figura 2 - Especificação do FIltro Digital passa-baixa.
No
segundo passo utilizaremos o dsPIC FD Lite, o Digital Filter Design
Software, para modelar o nosso filtro digital com estes parâmetros e
gerar os coeficientes para ser utilizado no programa do PIC32.
O método de realização do filtro, quantização, neste caso é "cascated second order sections". Estamos projetando um IIR FIlter Biquad, isto é, com 2 pólos e 2 zeros para cada seção do fiiltro.
No menu Design / IIR Design... iniciaremos o design para um Filtro Digital IIR.
Escolheremos o tipo de filtro: lowpass.
O método de realização do filtro, quantização, neste caso é "cascated second order sections". Estamos projetando um IIR FIlter Biquad, isto é, com 2 pólos e 2 zeros para cada seção do fiiltro.
No menu Design / IIR Design... iniciaremos o design para um Filtro Digital IIR.
Escolheremos o tipo de filtro: lowpass.
Na segunda tela, Figura 3, preencheremos os parâmetros do filtro passa-baixa conforme ilustrado anteriormente na Figura 2.
Figura 3 - Configurando os parâmetros para o filtro passa-baixa.
A Figura 4 mostra o resultado matemático para a modelagem do nosso filtro digital IIR passa-baixa de acordo com os parâmetros fornecidos.
Figura 4 - Resultado da Modelagem do Filtro Digital IIR lowpass.
Highpass IIR FIlter Design
A Figura 5 traz graficamente a representação de cada parâmetro do filtro highpass.
Figura 5 - Especificação do FIltro Digital passa-alta.
Os parâmetros do filtro passa-alta são configurados conforme a Figura 6.
Figura 6 - Configurando os parâmetros para o filtro passa-alta.
A Figura 7 mostra o resultado matemático para a modelagem do filtro digital IIR passa-alta.
Figura 7 - Resultado da Modelagem do Filtro Digital IIR highpass.
Bandpass IIR FIlter Design
A Figura 8 traz graficamente a representação de cada parâmetro do filtro bandpass.
Figura 8 - Especificação do FIltro Digital passa-banda.
Os parâmetros do filtro passa-banda são configurados conforme a Figura 9.
Figura 9 - Configurando os parâmetros para o filtro passa-banda.
A Figura 10 mostra o resultado matemático para a modelagem do filtro digital IIR passa-banda.
Figura 10 - Resultado da Modelagem do Filtro Digital IIR bandpass.
Bandstop IIR FIlter Design
A Figura 11 traz graficamente a representação de cada parâmetro do filtro bandstop.
Figura 11 - Especificação do FIltro Digital rejeita-banda.
Os parâmetros do filtro rejeita-banda são configurados conforme a Figura 12.
Figura 12 - Configurando os parâmetros para o filtro rejeita-banda.
A Figura 13 mostra o resultado matemático para a modelagem do filtro digital IIR rejeita-banda.
Figura 13 - Resultado da Modelagem do Filtro Digital IIR bandstop.
Gerando os coeficientes para o Filtro IIR
Clicando
no botão "Save C File" o software (dsPIC FD Lite - Digital Filter Design) irá gerar um código fonte padrão na
linguagem C para o filtro digital IIR construído, que pode ser visto no Código 1. Com ele você pode construir seu filtro DIgital IIR em outro
compilador C para computador ou outro modelo de microcontrolador.
/***************************************************************************
****************************************************************************
* File: E:\microchip_solutions_v2013-06-15\MyProjects\IIR FIlter\Digital Filter Design\Lowpass\lowpass1000Hz.c
* Created by dsPIC FD Lite Version 1.0.0 Build 1 at 21:20:05 May 04 2015
* C Code Generator - Version 4.0
****************************************************************************
* Code Fragment to implement filter
*
* The functions defined in 'qed_filt.c' must be compiled and linked in.
* This can be accomplished by either #include "qed_filt.c"
* or by separately compiling and linking 'qed_filt.c'
*
*** following is actual code fragment
* extern BiquadSections IIR_lowpass1000Hz;
*
* init_biquad_float (&IIR_lowpass1000Hz); // initialize filter structure
*
* IIR_lowpass1000Hz.filter ( x, y, n, &IIR_lowpass1000Hz); // x is an array of input samples
* // y is an array of output samples
* // n is number of samples to process
* // &IIR_lowpass1000Hz is a pointer to the
* // filter structure
*****************************************************************************
* This is a complete program which can be compiled and run to test the filter.
* To change this to a subroutine only, just add in this program or add globally
* in "qed_cgen.h" the line with the definition of DEFINE_SUBROUTINE as follows
* #define DEFINE_SUBROUTINE
*****************************************************************************
****************************************************************************/
/* qed_cgen.h contains definitions of filter structures and function prototypes */
#include "qed_cgen.h"
/* filter functions are in files 'qed_filt.c' */
float lowpass1000Hz_num[ 6] = {
9.454345703125e-002F, /* b[ 1, 0] */
1.891174316406e-001F, /* b[ 1, 1] */
9.454345703125e-002F, /* b[ 1, 2] */
6.185913085938e-002F, /* b[ 2, 0] */
1.237487792969e-001F, /* b[ 2, 1] */
6.185913085938e-002F}; /* b[ 2, 2] */
float lowpass1000Hz_den[ 6] = {
1.000000000000e+000F, /* a[ 1, 0] */
-8.160400390625e-001F, /* a[ 1, 1] */
1.943054199219e-001F, /* a[ 1, 2] */
5.000000000000e-001F, /* a[ 2, 0] */
-5.340270996094e-001F, /* a[ 2, 1] */
2.815856933594e-001F}; /* a[ 2, 2] */
float lowpass1000Hz_m1[2];
float lowpass1000Hz_m2[2];
float lowpass1000Hz_gain = 1.000000000000e+000F; /* initial gain for cascade realization */
/* also applies to parallel realization */
float lowpass1000Hz_pars = 1.000000000000e+000F; /* scale value for parallel sections */
BiquadSections IIR_lowpass1000Hz = {
2, /* number of sections */
0, /* realization method */
/* 0 Cascaded second order sections */
/* 1 Parallel second order sections */
1, /* quantization: 0 off, 1 on */
1, /* quantization type */
/* 0 Floating point */
/* 1 Fixed point fractional */
0, /* realization type for cascaded sections only */
/* 0 Fixed point - Transposed Canonic biquad sections */
/* 1 Fixed point - Canonic biquad sections */
/* 2 Floating point - 4 multiplies */
/* 3 Floating point - 5 multiplies */
/* 4 Floating point - recursive normal */
0, /* realization type for parallel sections only */
/* 0 Fixed point - Transposed Canonic biquad sections */
/* 1 Floating point - Transposed Canonic biquad sections */
&lowpass1000Hz_gain, /* pointer to gain for cascade/parallel realizations */
&lowpass1000Hz_pars, /* pointer to scale value for parallel sections */
lowpass1000Hz_num, /* pointer to numerator coefficients */
lowpass1000Hz_den, /* pointer to denominator coefficients */
lowpass1000Hz_m1, /* pointer to delay line 1 */
lowpass1000Hz_m2, /* pointer to delay line 2 */
cas_blkfloat_fm1}; /* ptr to filter routine */
/* call the following function first and normally only once */
/* init_biquad_float (&IIR_lowpass1000Hz) */
/* where &IIR_lowpass1000Hz is a pointer to the BiquadSections */
/* structure defining the filter */
/* call the following function to filter n samples */
/* IIR_lowpass1000Hz.filter (pIn, pOut, int n, &IIR_lowpass1000Hz); */
/* where pIn is a pointer to an array or buffer of samples to be filtered */
/* pOut is a pointer to the array of filtered samples output by the filter */
/* n is the number of samples to filter */
/* &IIR_lowpass1000Hz is a pointer to the structure defining the filter */
#ifndef DEFINE_SUBROUTINE
/* The following main program can be used to test the filter. */
/* input is in file 'in' and the filtered samples are in file 'out' */
/* The input and output files are ascii floating point values */
/* e.g 1.0342 with 1 sample per line */
/* The input files can be created in DSPworks and exported as */
/* ascii floating point or any other system capable of creating */
/* ascii files with floating point values. */
/* The filtered output file can be imported into DSPworks as an ascii */
/* floating point file and an FFT can be run to validate */
/* the frequency response. */
#include "qed_filt.c"
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#define INSZ1 1000
#define OUTSZ1 1000
static float x[INSZ1], y[OUTSZ1];
int main(int argc, char *argv[])
{
int i, in_count, file_status, error;
FILE *fin; /* input file of samples */
FILE *fout; /* output file of filtered samples */
fprintf (stderr," ***** start filter test *****\n");
fprintf (stderr," this program accepts 0,1 or 2 command line arguments\n");
fprintf (stderr," the first argument is the filename of the input file\n");
fprintf (stderr," the second argument is the filename of the output file\n");
fprintf (stderr," if there are 0 arguments, input and output is respectively\n");
fprintf (stderr," stdin and stdout\n");
fprintf (stderr," if only one argument is specified, then output is stdout\n");
fprintf (stderr," if input is stdin rather than a file, then fscanf expects input\n");
fprintf (stderr," from the console which may be piped in or entered directly\n");
fin = stdin;
fout = stdout;
error = 0;
if (argc == 1) {
fprintf(stderr," ***** waiting for input *****\n");
}
if (argc >= 2) {
fin = fopen (argv[1], "r");
if (fin == NULL) {
fprintf(stderr,"\n error - Cannot open file %s for input\n", argv[1]);
error = 1;
}
}
if (argc >= 3) {
fout = fopen (argv[2], "w");
if (fout == NULL) {
fprintf(stderr,"\n error - Cannot open file %s for output\n", argv[2]);
error = 1;
}
}
if (error) {
fprintf(stderr," ***** end filter test *****\n");
return(0);
}
init_biquad_float (&IIR_lowpass1000Hz);
do {
/* get input samples */
for (in_count = 0; in_count < INSZ1; in_count++) {
file_status = fscanf(fin,"%f",&x[in_count]);
if (file_status != 1)
break;
}
/* filter samples */
if (in_count == 0) break;
IIR_lowpass1000Hz.filter( x, y, in_count, &IIR_lowpass1000Hz);
for (i = 0; i < in_count; i++)
fprintf (fout,"%f\n",y[i]);
} while (file_status == 1);
fclose (fin);
fclose (fout);
fprintf(stderr," ***** end filter test *****\n");
return(1);
}
#endif
Código 1 - Código C gerado com coeficientes para o Filtro IIR Lowpass.
O que nos interessa neste código são os valores dos coeficientes A1, A2, B1 e B2, que iremos utilizar no programa do PIC32MX. "A" e "B" são os pólos e zeros do Filtro.
Os valores dos coeficientes estão identificados em formato de matriz:
Coeficiente [ número da seção Biquadrada , número do coeficiente ]
Exemplo:
A [1,1] = coeficiente A1 da primeira seção biquadrada.
A [1,2] = coeficiente A2 da primeira seção biquadrada.
A [2,1] = coeficiente A1 da segunda seção biquadrada.
A [2,2] = coeficiente A2 da segunda seção biquadrada.
B [1,1] = coeficiente B1 da primeira seção biquadrada.
B [1,2] = coeficiente B2 da primeira seção biquadrada.
B [2,1] = coeficiente B1 da segunda seção biquadrada.
B [2,2] = coeficiente B2 da segunda seção biquadrada.
O IIR FIlter Biquad possui 2 pólos e 2 zeros para cada seção (seções de segunda ordem).
Para o Filtro IIR, A0 não é utilizado na função mips_iir16 ( ) da biblioteca DSP Library com o PIC32MX.
B0 não é necessário ser informado na função mips_iir16 ( ) da biblioteca DSP Library para o PIC32, pois no IIR FIlter Biquad, B0 = B2.
Por isto, no programa do PIC32MX, iremos utilizar somente os coeficientes A1, A2, B1 e B2 de cada seção.
Estamos modelando um Filtro Analógico Butterworth de 4ª ordem. Temos então 4 pólos e 4 zeros.
No menu Codegen / Microchip / dsPIC30 iremos gerar o código em Assembly com os coeficientes. Este código com os coeficientes para o filtro IIR lowpass é visto no Código 2.
; ..............................................................................
; File lowpass1000Hz.s
; ..............................................................................
.equ lowpass1000HzNumSections, 2
; ..............................................................................
;
; Allocate and initialize filter coefficients
;
; These coefficients have been designed for use in the Transpose filter only
.section .xdata
lowpass1000HzCoefs:
.hword 0x060D ; b( 1,0)/2
.hword 0x0C1A ; b( 1,1)/2
.hword 0x343A ; a( 1,1)/2
.hword 0x060D ; b( 1,2)/2
.hword 0xF391 ; a( 1,2)/2
.hword 0x07EB ; b( 2,0)/2
.hword 0x0FD7 ; b( 2,1)/2
.hword 0x445B ; a( 2,1)/2
.hword 0x07EB ; b( 2,2)/2
.hword 0xDBF5 ; a( 2,2)/2
; ..............................................................................
; Allocate states buffers in (uninitialized) Y data space
.section .ybss, "b"
lowpass1000HzStates1:
.space lowpass1000HzNumSections*2
lowpass1000HzStates2:
.space lowpass1000HzNumSections*2
; ..............................................................................
; Allocate and intialize filter structure
.section .data
.global _lowpass1000HzFilter
_lowpass1000HzFilter:
.hword lowpass1000HzNumSections-1
.hword lowpass1000HzCoefs
.hword 0xFF00
.hword lowpass1000HzStates1
.hword lowpass1000HzStates2
.hword 0x0000
; ..............................................................................
; Sample assembly language calling program
; The following declarations can be cut and pasted as needed into a program
; .extern _IIRTransposeFilterInit
; .extern _BlockIIRTransposeFilter
; .extern _lowpass1000HzFilter
;
; .section .bss
;
; The input and output buffers can be made any desired size
; the value 40 is just an example - however, one must ensure
; that the output buffer is at least as long as the number of samples
; to be filtered (parameter 4)
;input: .space 40
;output: .space 40
; .text
;
;
; This code can be copied and pasted as needed into a program
;
;
; Set up pointers to access input samples, filter taps, delay line and
; output samples.
; mov #_lowpass1000HzFilter, W0 ; Initalize W0 to filter structure
; call _IIRTransposeFilterInit ; call this function once
;
; The next 4 instructions are required prior to each subroutine call
; to _BlockIIRTransposeFilter
; mov #_lowpass1000HzFilter, W0 ; Initalize W0 to filter structure
; mov #input, W1 ; Initalize W1 to input buffer
; mov #output, W2 ; Initalize W2 to output buffer
; mov #20, W3 ; Initialize W3 with number of required output samples
; call _BlockIIRTransposeFilter ; call as many times as needed
Este procedimento deve ser repetido para os 4 tipos de filtro IIR: lowpass, highpass, bandpass e bandstop. Os coeficientes A1, A2, B1 e B2 são diferentes para cada design elaborado.
O Hardware
Neste projeto utilizaremos:
a) PIC32MX USB Starter Kit II;
b) I/O Expansion Board;
c) GFXv3 Graphic Display.
O PIC32 irá gerar um sinal senoidal de frequência variável, aplicar o filtro digital IIR, calcular a Transformada Rápida de Fourier, a fim de verificar a resposta de cada tipo de filtro e comparar com os dados teóricos obtidos com o dsPIC FD Lite e mostrar no display os respectivos gráficos.
O código fonte do PIC32
No terceiro passo elaboraremos o programa do PIC no compilador MPLAB C32 da Microchip com o ambiente de desenvolvimento MPLAB X. O Programa foi desenvolvido em linguagem C.
Incluímos em nosso projeto a biblioteca "dsplib_dsp.h" que possui as funções para o cálculo dos filtros digitais IIR, FIR e outras utilizadas em cálculos de processamentos digitais, como a FFT.
O Código 3 mostra a inclusão da biblioteca e a declaração dos vetores do Filtro Digital IIR.
Os coeficientes são carregados para A1, A2, B1 e B2 de acordo com o tipo de filtro selecionado: lowpass, highpass, bandpass ou bandstop.
Primeiro deve-se iniciar com zero o vetor delayline [ ].
Depois carregam-se os valores dos coeficientesem bq [ ], de acordo com o tipo do filtro IIR selecionado.
Agora então podemos chamar a função mips_iir16_setup ( ) da biblioteca DSP do PIC32MX que se encarrega de inicializar a estrutura do filtro IIR.
O Código 5 mostra a aplicação do filtro propriamente dito em uma amostra do sinal de entrada.
A função responsável pelo cálculo do Filtro IIR Biquad é a mips_iir16 ( ), e pertence à DSP Library da Microchip para o PIC32MX.
Nosso programa executa o Código 6 em um loop infinito: gera uma onda senoidal de frequência variável; aplica o filtro IIR ao sinal gerado; calcula a FFT ao sinal Filtrado e atualiza o display com os gráficos.
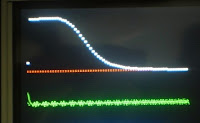
O resultado final do nosso projeto é visto na Figura 14. Interligando um display gráfico QVGA 320x240 vemos o sinal gerado sendo aplicado ao Filtro Digital IIR.
A Figura 15 mostra a resposta na prática para o nosso filtro passa-baixa de 1000 Hz.
A Figura 16 mostra a resposta na prática para o nosso filtro passa-alta de 2000 Hz.
A Figura 17 mostra a resposta na prática para o nosso filtro passa-banda de 1500 Hz à 2000 Hz.
A Figura 18 mostra a resposta na prática para o nosso filtro rejeita-banda de 2000 Hz à 2500 Hz
Estas curvas podem ser comparadas com aquelas do início deste post, geradas pelo dsPIC FD Lite, a fim de verificar a performance do Filtro Digital IIR da DSP Library com o PIC32MX!
#include "dsplib_dsp.h" // library to FFT and IIR FIlter functions
// vetores para iir filter
#define B 2 //2 Biquad Sections
biquad16 bq[B];
int16 coeffs[4*B];
int16 delayline[2*B];
int16 indata, outdata;
int16 sinal_Filtrado [N*2];
Código 3 - Incluindo a biblioteca DSP e declarando os vetores.
Após
o início do programa, na função main ( ) temos que iniciar as variáveis
e atribuir os coeficientes do filtro. Os valores para A1, A2, B1 e B2
foram retirados do código Assembly gerado pelo dsPIC Filter Design Lite.
A inicialização das variáveis e coeficientes são vistos no Código 4.
A inicialização das variáveis e coeficientes são vistos no Código 4.
Os coeficientes são carregados para A1, A2, B1 e B2 de acordo com o tipo de filtro selecionado: lowpass, highpass, bandpass ou bandstop.
int main(void)
{
...
// inicializa componentes de hardware e periféricos
InitializeBoard();
while(1)
{
// carrega coeficientes de acordo com o filtro selecionado
iir_coefficients_setup ();
...
...
...
}
}
void iir_coefficients_setup ()
{
int i;
//inicializa com zero delayline do iir filter
for (i = 0; i < 2*B; i++)
delayline[i] = 0;
/* altera coeficientes do filtro IIR conforme a selecao */
// load coefficients into bq here
switch (filterType) {
case FILTER_OFF:
break;
case LOWPASS:
bq [0].a1 = 0x343A; //a( 1,1)/2
bq [0].a2 = 0xF391; //a( 1,2)/2
bq [0].b1 = 0x0C1A; //b( 1,1)/2
bq [0].b2 = 0x060D; //b( 1,2)/2
bq [1].a1 = 0x445B; //a( 2,1)/2
bq [1].a2 = 0xDBF5; //a( 2,2)/2
bq [1].b1 = 0x0FD7; //b( 2,1)/2
bq [1].b2 = 0x07EB; //b( 2,2)/2
break;
case HIGHPASS:
bq [0].a1 = 0xFBAF; //a( 1,1)/2
bq [0].a2 = 0xFD67; //a( 1,2)/2
bq [0].b1 = 0xE0DC; //b( 1,1)/2
bq [0].b2 = 0x0F92; //b( 1,2)/2
bq [1].a1 = 0xFA00; //a( 2,1)/2
bq [1].a2 = 0xE360; //a( 2,2)/2
bq [1].b1 = 0xD4B0; //b( 2,1)/2
bq [1].b2 = 0x15A7; //b( 2,2)/2
break;
case BANDPASS:
bq [0].a1 = 0xFF3C; //a( 1,1)/2
bq [0].a2 = 0xD061; //a( 1,2)/2
bq [0].b1 = 0x0000; //b( 1,1)/2
bq [0].b2 = 0xF7D0; //b( 1,2)/2
bq [1].a1 = 0x1FDD; //a( 2,1)/2
bq [1].a2 = 0xCFC9; //a( 2,2)/2
bq [1].b1 = 0x0000; //b( 2,1)/2
bq [1].b2 = 0xEFDC; //b( 2,2)/2
break;
case BANDSTOP:
bq [0].a1 = 0x91BB; //a( 1,1)/2
bq [0].a2 = 0xCF87; //a( 1,2)/2
bq [0].b1 = 0xFFD1; //b( 1,1)/2
bq [0].b2 = 0x0102; //b( 1,2)/2
bq [1].a1 = 0x7135; //a( 2,1)/2
bq [1].a2 = 0xCD3B; //a( 2,2)/2
bq [1].b1 = 0xECE9; //b( 2,1)/2
bq [1].b2 = 0x6872; //b( 2,2)/2
break;
default :
break;
}
mips_iir16_setup(coeffs, bq, B);
}
Còdigo 4 - Carregando os coeficientes e inicializando a estrutura do Filtro IIR.
Primeiro deve-se iniciar com zero o vetor delayline [ ].
Depois carregam-se os valores dos coeficientesem bq [ ], de acordo com o tipo do filtro IIR selecionado.
Agora então podemos chamar a função mips_iir16_setup ( ) da biblioteca DSP do PIC32MX que se encarrega de inicializar a estrutura do filtro IIR.
O Código 5 mostra a aplicação do filtro propriamente dito em uma amostra do sinal de entrada.
/* calculate iir filter biquad */
void iir_filter ()
{
int i;
for (i=0;i<N*2;i++)
{
// get input data value into indata
indata = sine_wave_input[i] ;
//calculate iir filter biquad
outdata = mips_iir16(indata, coeffs, delayline, B, 1);
sinal_Filtrado [i] = outdata;
} //end for
}
Código 5 - Função que aplica o FIltro IIR ao sinal de entrada.
A função responsável pelo cálculo do Filtro IIR Biquad é a mips_iir16 ( ), e pertence à DSP Library da Microchip para o PIC32MX.
Nosso programa executa o Código 6 em um loop infinito: gera uma onda senoidal de frequência variável; aplica o filtro IIR ao sinal gerado; calcula a FFT ao sinal Filtrado e atualiza o display com os gráficos.
sineWaveGeneration (signal_freq, 7680.0 ); //gera sinal senoidal
iir_filter (); //aplica o filtro iir ao sinal gerado
moveVectorInputFFT (); //move sinal gerado para entrada do calculo da FFT
fftCalculate (); //calcula a FFT do sinal gerado
updateDisplay (); //atualiza a tela
Código 6 - Loop do programa no código main.
O resultado final do nosso projeto é visto na Figura 14. Interligando um display gráfico QVGA 320x240 vemos o sinal gerado sendo aplicado ao Filtro Digital IIR.
Figura 14 - Sinais sendo mostrados no display gráfico.
A Figura 15 mostra a resposta na prática para o nosso filtro passa-baixa de 1000 Hz.
Figura 15 - Resposta do IIR FIlter lowpass.
A Figura 16 mostra a resposta na prática para o nosso filtro passa-alta de 2000 Hz.
Figura 16 - Resposta do IIR FIlter highpass.
A Figura 17 mostra a resposta na prática para o nosso filtro passa-banda de 1500 Hz à 2000 Hz.
Figura 17 - Resposta do IIR FIlter bandpass.
A Figura 18 mostra a resposta na prática para o nosso filtro rejeita-banda de 2000 Hz à 2500 Hz
Figura 18 - Resposta do IIR FIlter bandstop.
Lembrando que a frequência de amostragem é 7680 Hz e o sinal gerado varia de 0 à 3840 Hz, respeitrando o Teorema de Nyquist.
O Vídeo 1 mostra o projeto do Filtro Digital IIR elaborado no MPLAB X e rodando com o PIC32MX.
Vídeo 1 - IIR FIlter com PIC32MX.
Os cálculos da Fast Fourier Transform (FFT) para o PIC32MX você encontra aqui.
Referências:
ORFANIDS, Sophocles J. Introduction to Signal Processing. Pearson Education/Prentice Hall/Sophocles J. Orfanidis.2009. Disponível em: http://www.ece.rutgers.edu/~orfanidi/intro2sp
PALACHERLA, Amar. Implementing IIR Digital Filters. Application Note AN540. Microchip Technology Inc.1997.
RAMU, B. K. Anantha. Implementing FIR and IIR Digital Filters using PIC18 microcontrollers. Application Note AN852. Microchip Technology Designs. India. 2002.
SKANDA, Vinaya. Sine Wave Generator Using Numerically Controller PIC. Application Note AN1523A. Microchip Technology Inc. 2013.
HAYKIN, Simon S.; VAN VEEN, Barry. Sinais e sistemas. Porto Alegre: Bookman, 2001. 668p.
MANCHESTER. Z-transforms & IIR-type digital filters. University of Manchester. School of Computer Science. Digital Media Processing. Section 5. 2009. 19p. Disponível em: www.cs.man.ac.uk/~barry/mydocs/COMP30291/Notes/DMP09-5.doc
MICROCHIP. Using the Fast Fourier Transform (FFT) for Frequency Detection. Code Examples CE018. Microchip Technology Inc. Disponível em: http://ww1.microchip.com/downloads/en/DeviceDoc/CE018_FFT_DSPlib_101007.zip
MICROCHIP. Software Libraries. Disponível em: http://www.microchip.com/SoftwareLib.aspx
MICROCHIP. PIC32 DSP Library. Disponível em: http://www.microchip.com/stellent/idcplg?IdcService=SS_GET_PAGE&nodeId=2680&dDocName=en552827
Anexo A
Código básico para aplicar o cálculo de 1 tipo de Filtro Digital IIR.
#include "dsplib_dsp.h" // library to FFT and IIR FIlter functions
// vetores para iir filter
#define B 2 //2 Biquad Sections
biquad16 bq[B];
int16 coeffs[4*B];
int16 delayline[2*B];
int16 indata, outdata;
int16 sinal_Filtrado [N*2];
int main(void)
{
...
// inicializa componentes de hardware e periféricos
InitializeBoard();
// carrega coeficientes de acordo com o filtro selecionado
iir_coefficients_setup ();
while(1)
{
iir_filter (); //aplica o filtro iir ao sinal gerado
...
...
...
}
}
void iir_coefficients_setup ()
{
int i;
//inicializa com zero delayline do iir filter
for (i = 0; i < 2*B; i++)
delayline[i] = 0;
// load coefficients into bq here
bq [0].a1 = 0x343A; //a( 1,1)/2
bq [0].a2 = 0xF391; //a( 1,2)/2
bq [0].b1 = 0x0C1A; //b( 1,1)/2
bq [0].b2 = 0x060D; //b( 1,2)/2
bq [1].a1 = 0x445B; //a( 2,1)/2
bq [1].a2 = 0xDBF5; //a( 2,2)/2
bq [1].b1 = 0x0FD7; //b( 2,1)/2
bq [1].b2 = 0x07EB; //b( 2,2)/2
mips_iir16_setup(coeffs, bq, B);
}
/* calculate iir filter biquad */
void iir_filter ()
{
int i;
for (i=0;i<N*2;i++)
{
// get input data value into indata
indata = sine_wave_input[i] ;
//calculate iir filter biquad
outdata = mips_iir16 (indata, coeffs, delayline, B, 1);
sinal_Filtrado [i] = outdata;
} //end for
}